Harmonogramowanie produkcji i procesów przemysłowych

Harmonogramowanie produkcji oraz dostatecznie szybkie reagowanie na zmiany w otoczeniu firmy zawsze jest wyzwaniem. Wraz ze zwiększająca się potrzebą tworzenia produktów w wyspecjalizowanych fabrykach (niezależnie od przemysłu), wzrosła również potrzeba na specjalne harmonogrowanie procesów przemysłowych. Systemy te muszą, niezależnie od wielkości przedsiębiorstwa, pomagać użytkownikom w planowaniu pracy tak, aby wszystkie zlecenia były realizowane w wyznaczonym czasie, a ogólna wydajność sprzętu była jednocześnie monitorowana i usprawniana.
Dla małych przedsiębiorstw produkcja może być planowana z ogromną precyzją przy wykorzystaniu prostych narzędzi, zgodnie z wymaganiami użytkownika szukającego optymalnego rozwiązania z dedykowanego systemu. Dla większej firmy z dziesiątkami linii produkcyjnych i zamówieniami liczonymi w setkach każdego dnia pewien margines błędu jest akceptowalny, gdyż obiektem zainteresowania jest zoptymalizowanie problemów trudnych do rozwiązania człowiekowi. Dla obu typów użytkowników, odpowiedzialność takiego systemu jest wyjątkowo ważna, a plan powinien być sporządzony w kilka sekund, aby nie zniechęcić do używania oprogramowania. Dodatkowo, jeśli czas oczekiwania na plan jest zbyt długi, może się okazać, że w międzyczasie nowe zamówienia zostały zaakceptowane, natomiast on stał się nieaktualny, jeszcze zanim został stworzony. W artykule opiszę jeden ze sposobów dotarcia do problemu, aby wynik planowania był satysfakcjonujący zarówno dla małych, jak i dużych przedsiębiorstw.
Spis treści:
- Czym dokładnie jest harmonogramowanie produkcji i procesów przemysłowych?
- Jakość a czas obliczeń
- Heurystyki na ratunek!
- Harmonogramowanie produkcji – siła liczb i działań
Czym dokładnie jest harmonogramowanie produkcji i procesów przemysłowych?
Opisywany problem oparty jest na dobrze znanym zagadnieniu planowania w małych systemach produkcyjnych. Jest to zagadnienie dotyczące optymalizowania produkcji, w którym sprzęt oraz wykonywane prace zawarte są w uporządkowanej sekwencji działań. Czas ukończenia zadań wykonywanych przez maszynę jest znany, potrzebne jest więc określenie momentu rozpoczęcia pracy oraz urządzenia dedykowanego każdej z operacji, aby cały proces produkcyjny została wykonany tak szybko, jak jest to możliwe. Kluczowe jest, aby zachowana została kolejność operacji oraz, aby więcej niż dwa zadania nie były wykonywane jednocześnie na tej samej maszynie.
Podane zagadnienie dotyczące znajdowania właściwych sekwencji zadań jest jedynie teoretyczną podstawą dla wyzwań występujących w rzeczywistości. Dla przykładu, przyjrzyjmy się głębiej problemowi drukowania książek dla dzieci. Zanim produkt trafi do sklepu, wykonanych musi zostać kilka zróżnicowanych operacji.
Po pierwsze strony są drukowane. Część z nich może zawierać dodatkowe zdobienia. Często kilka z nich jest drukowanych na jednej kartce papieru, która następnie jest cięta, aby je odseparować. Okładka jest tworzona niezależnie od tego procesu, a następnie łączona z wydrukowaną zawartością książki. Cały produkt jest w końcu odpowiednio pakowany.
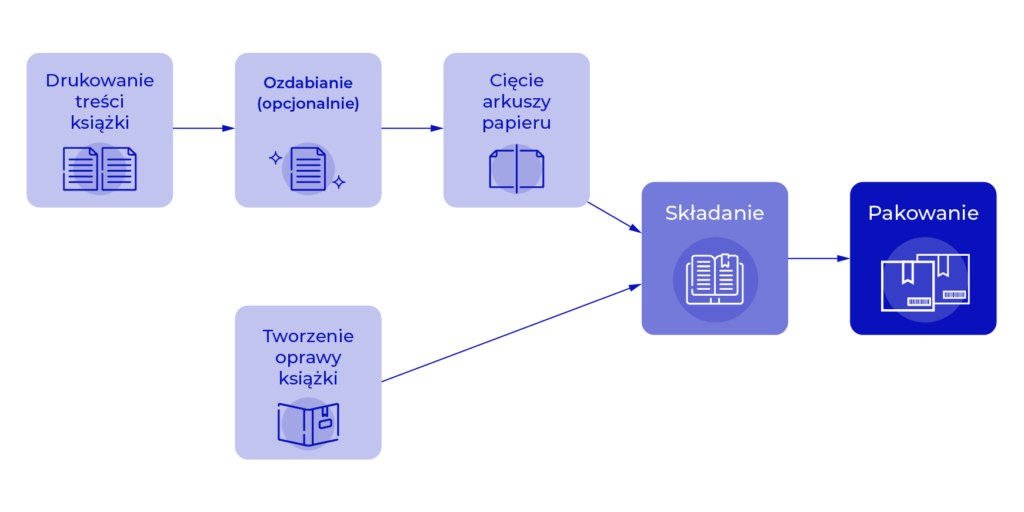
Jak można zauważyć, część z czynności wykonywana jest jako logiczne następstwa, inne, takie jak tworzenie okładki i drukowanie treści, mogą być prowadzone jednocześnie, a jeszcze inne, takie jak ozdabianie, są opcjonalne. W przedsiębiorstwie nie ma dostępnego całego materiału, co wywołuje dodatkowe ograniczenia logistyczne. Patrząc na temat całościowo, zamówienia muszą także zostać zrealizowane w terminie, co również ma wpływ na planowanie.
Wiemy już, czym jest harmonogramowanie produkcji i procesów przemysłowych, ale jaki efekt wywołuje zwiększenie liczby wymagań na potencjalnego planującego? Zarówno złożoność, jak i rozmiar zadania są wśród głównych czynników wpływających na czas potrzebny do stworzenia planu. Przyjrzyjmy się bliżej relacji między zadaniem a czasem potrzebnym do jego wykonania.
Jakość a czas obliczeń w harmonogramowaniu procesów przemysłowych
Wspomniałem już o tym, że głównym determinantem czasu, który algorytm wykorzysta na przetwarzanie, jest złożoność zadania (relacja między zadaniami a dodatkowymi ograniczeniami) oraz rozmiarem problemu (w przykładzie z książkami dla dzieci jest to liczba zamówień oraz liczba dostępnych maszyn). Spójrzmy na to, w jaki sposób zagadnienie to zostanie rozwiązane z użyciem algorytmu Integer Linear Programming (ILP), aby lepiej zrozumieć, dlaczego tak jest.
ILP w harmonogramowaniu procesów przemysłowych używane jest do zoptymalizowania problemów, które mogą zostać zapisane z użyciem nierówności (ograniczeń) i pokazać optymalne rozwiązanie, minimalizując funkcję celu. Dla przykładu, aby odnaleźć prostokąt z najmniejszym polem, którego suma boków musi być większa niż dziesięć, ale żaden z nich nie może być mniejszy niż 1, stworzylibyśmy trzy równania. Nazwijmy boki prostokąta a oraz b, z czego wychodzi:
Celem funkcji byłoby zminimalizowanie iloczynu a i b.
W jaki sposób równania, zmienne i funkcje celu są związane z kwestią szeregowania? Zacznijmy od określenia, czym są niewiadome, których poszukujemy. Aby stworzyć plan, musimy wiedzieć, kiedy każda z operacji musi się rozpocząć (ponieważ wiemy, jak długo trwa, oraz na której z maszyn może zostać wykonana). Równania będą ograniczać możliwe wyniki. Dla przykładu, cięcie papieru musi zostać wykonane po wydrukowaniu tekstu, co może zostać zapisane jako:
(czas rozpoczęcia drukowania) + (czas drukowania =< (czas rozpoczęcia cięcia papieru)
Jaka jest wtedy nasza funkcja celu? Zastosowane mogą być różne strategie, jednak najprostszym sposobem, aby stworzyć dobry plan, jest zminimalizowanie ogólnego czasu produkcji. Dlatego naszą funkcją celu jest zminimalizowanie czasu zakończenia ostatniej produkcji.
Tak zdefiniowany przykład problem może zostać przekazany do wyspecjalizowanego solvera. Liczba niewiadomych zależy w dużej mierze od liczby zadań, natomiast liczba równań jest również związana z liczbą ograniczeń wynikających ze złożoności naszego zadania.
Nasuwa się pytanie – czy wydłużenie czasu w pewnym momencie staje się nie do zaakceptowania? Jak widzimy na ilustracji nr 2, w kolejnych 50 zadaniach testowych, wydłużenie czasu dla algorytmu dostarczającego dokładne rozwiązanie jest wykładnicze, więc czas obliczeń z minut szybko przechodzi w godziny, a następnie – w dni. Co możemy więc zrobić, aby znaleźć rozwiązanie dla tak dużych zadań?
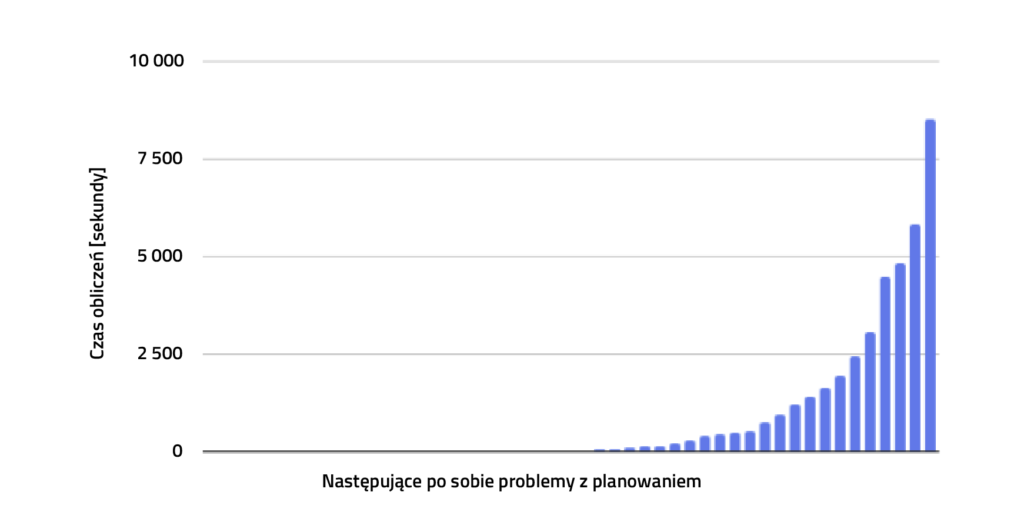
Ilustracja. 2 Wzrost w czasie jako funkcja rozmiaru zadania dla algorytmu zawierającego optymalne rozwiązanie
Heurystyki na ratunek!
Algorytmy heurystyczne charakteryzują się znacznie większą wydajnością czasową i są często wybierane do dużych zadań. Związana z nimi trudność łączy się z wyborem odpowiednich parametrów, aby rezultaty były tak bliskie optymalnego wyniku, jak jest to możliwe. Przykładem algorytmu heurystycznego dla planowania są Dispatch Rules (DR). Polegają na stworzeniu pustego planu, a następnie wybraniu iteracyjnie jednego zadania i umieszczeniu go na planie.
Jest to tak proste, że mógłbyś zaplanować produkcję na kartce papieru! Gdzie jest więc cała złożoność? Problemem jest strategia wyboru odpowiedniego zadania dla każdego kroku, aby otrzymać jak najlepszy wynik. Aby wybrać najlepszą operację w danym kroku, potrzebna jest nam reguła dokonywania selekcji, np. wybór najkrótszego zadania. Czy pojedyncza reguła wystarczy? Co jeśli wiele zadań jest „najlepszych”? Sposobem na poradzenie sobie z tym problemem jest stworzenie uporządkowanego zestawu reguł, tak że jeśli istnieje więcej niż jedno najlepsze zadanie zgodnie z daną regułą, dalsze reguły są stosowane do podzbioru wcześniej wybranych zadań, aż zostanie wybrane dokładnie jedno zadanie. Zobaczmy, jak mogłaby wyglądać taka lista:
- wybierz zadanie, które ma najkrótszy czas oczekiwania na rozpoczęcie produkcji,
- wybierz zadanie o najkrótszym czasie trwania,
- wybierz zadanie o najmniejszym numerze identyfikacyjnym.
Tym sposobem, nasz plan osiągany jest w szybki sposób. Jak szybki w porównaniu do tego samego zadania, które widzieliśmy w ilustracji nr 2? Odpowiedź jest widoczna w ilustracji nr 3.
Gdzie podział się czerwony kolor oznaczający czas przetwarzania reguł wysyłki? Najlepsze jest to, że jest tak krótki, że zajmuje tylko kilka sekund, nawet w przypadku dużych zadań!
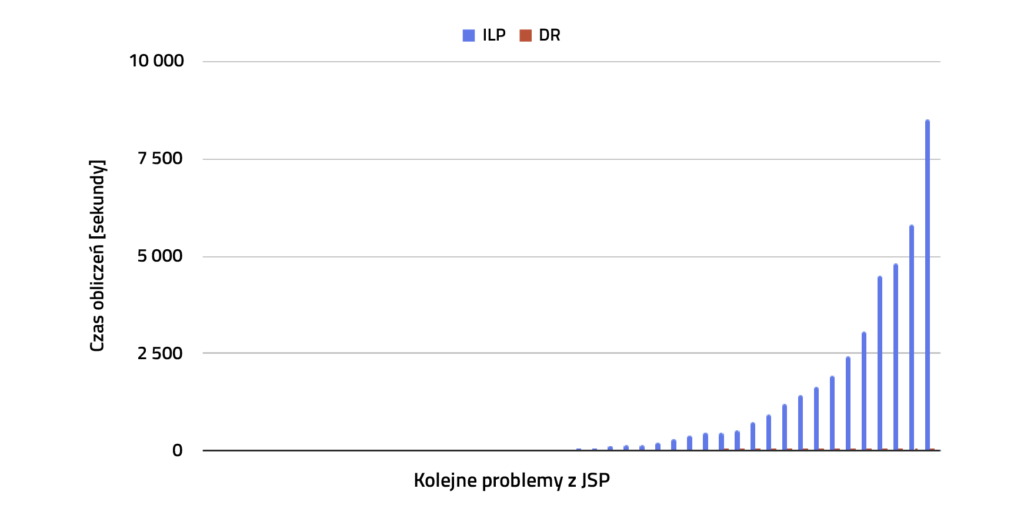
Ilustracja 3. Czas obliczania harmonogramu produkcji dla obu algorytmów.
Jaka jest różnica między uzyskanym czasem trwania planu? Użyjmy większego zestawu 150 produkcji i zobaczmy rysunek 4. Wyraźnie widać, że DR z określonego rozmiaru problemu ma tendencję do uzyskiwania znacznie gorszych wyników.
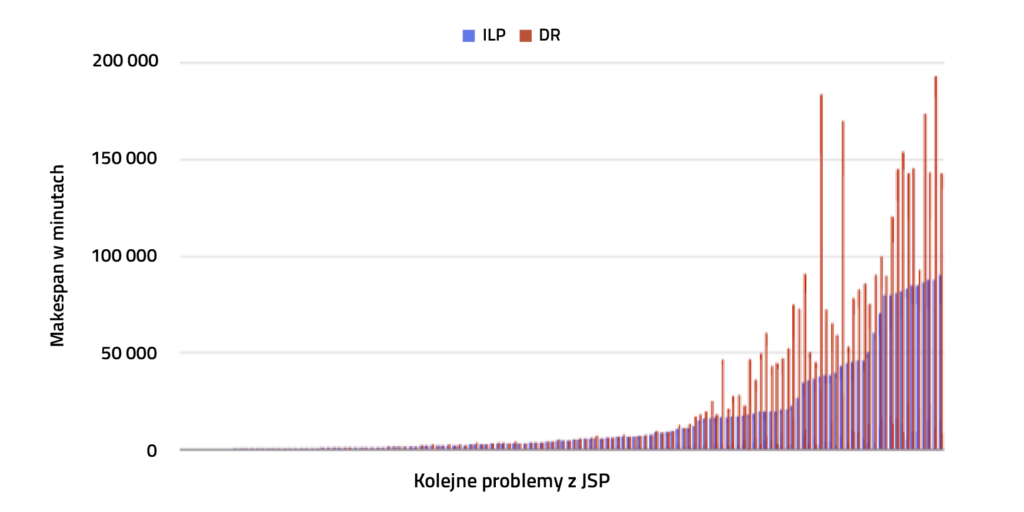
Jeśli utworzymy metrykę z połączonych wartości czasu trwania planu algorytmu i czasu wykonania, możemy zobaczyć, jak dobry jest dany algorytm. Wyniki można zobaczyć na rysunku 5. Widać wyraźnie, że dla małych zadań ILP w harmonogramowaniu procesów przemysłowych jest lepszy, wtedy oba algorytmy mają podobne wyniki, a następnie reguły wysyłania są wyraźnie lepsze dla dużych problemów. Chcieliśmy jednak uzyskać jedną metodę na wszystkie problemy – co możemy teraz zrobić?
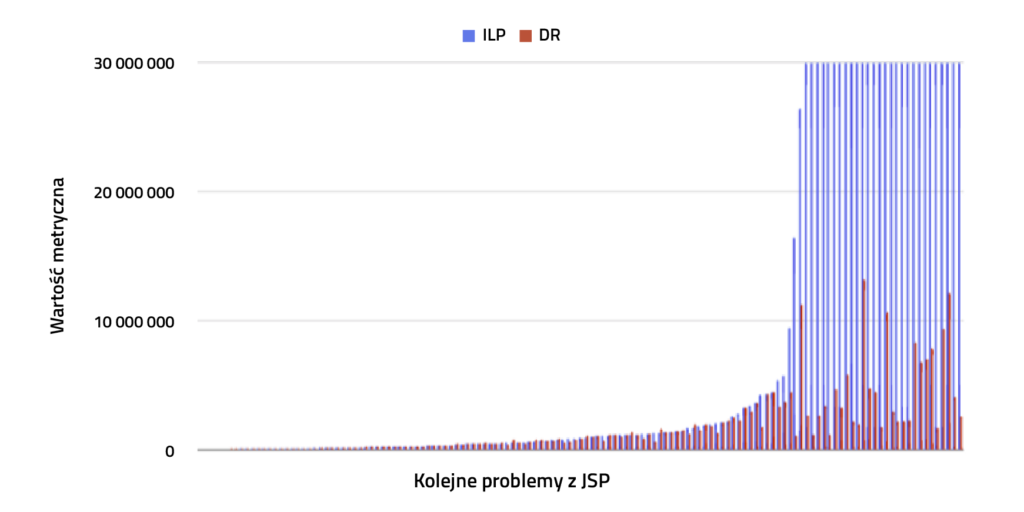
Ilustracja 5. Zsumowane wartości czasu wykonania planu i czasu wykonania dla kolejnych problemów harmonogramowania (posortowane według wyniku ILP).
Harmonogramowanie produkcji – siła liczb i działań
Odpowiedzią jest użycie obu algorytmów! W jaki sposób? Stworzymy moduł decyzyjny, aby dobrać odpowiedni algorytm dla danego problemu planowania. Decyzja zostanie podjęta na podstawie charakterystyki problemu. Liczba operacji, zadań, maszyn i szereg ograniczeń zostanie wykorzystana do oceny, która metoda najlepiej pasuje do przypadku.
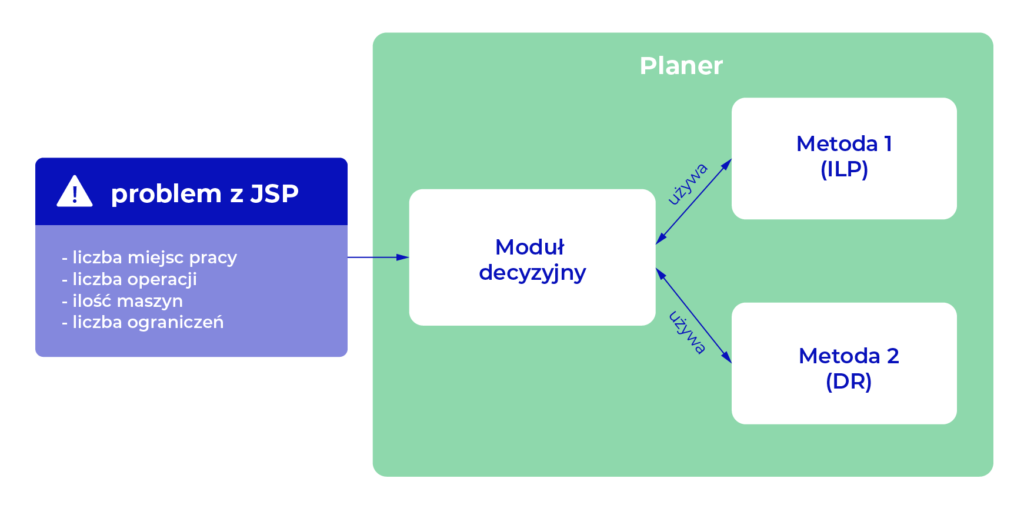
Ilustracja 6. Schemat harmonogramu produkcji zwraca najlepszy plan, biorąc pod uwagę zarówno jakość, jak i czas tworzenia.
Moduł decyzyjny (przy użyciu drzew decyzyjnych) przetestowany na 150 przykładach uczących uzyskał dokładność około 90 procent na 50-elementowym zbiorze testowym. Co oznacza ten wynik? W 90% przypadków najlepszy wynik został wybrany z dwóch możliwych, ale nie oznacza to, że wynik ten jest niepoprawny dla pozostałych przypadków. Plan stworzony dla 10% problemów był gorszy o co najwyżej 20% w porównaniu z lepszym rozwiązaniem. Przypadki te wystąpiły w przestrzeni, w której różnica między wynikami była nieznaczna.
W efekcie mamy harmonogram zbudowany z dwóch metod, który z dużą dokładnością radzi sobie z wyborem lepszego algorytmu. Jego dodatkową zaletą jest możliwość dodania większej liczby metod w razie potrzeby. Oprogramowanie do planowania zawierające tak wszechstronne narzędzie zapewni zatem użytkownikowi wysokiej jakości plan produkcji w czasie, który nie zniechęci go do korzystania z oprogramowania. Poznaj również możliwości systemu Nexelem do planowania produkcji!
Organizacja produkcji to kluczowy aspekt, który pozwoli ci na wykorzystanie w pełni możliwości swojej firmy. Dowiedz się więcej z nami!